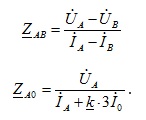Моделирование устройств РЗиА: реле сопротивления

Дистанционная защита срабатывает по сопротивлениям контуров фаза-фаза для защиты от междуфазных КЗ или по контуру фаза-земля для защиты от коротких замыканий на землю в сети с заземленной нейтралью.
Линейные комбинации токов и напряжения выбираются таким образом, чтобы замер дистанционного органа был пропорционален расстоянию до точки металлического КЗ. Для примера:

В дальнейшем изложении будем считать, что мы уже имеем ортогональные составляющие напряжения и тока, которые заранее рассчитаны для вычисления сопротивления. Тогда формула для расчета сопротивления будет выглядеть следующим образом:

Ее можно использовать как для дальнейших расчетах в дистанционных реле, так и просто для индикации. В случае только индикации этот расчет можно выполнять в более медленном темпе, чем расчеты для работы алгоритмов защиты.
Характеристикой срабатывания дистанционной защиты в комплексной плоскости является область, ограниченная линией, заданной пользователем с помощью уставок, таких как угол линии, полное сопротивления, активное сопротивление.
Несмотря на возможные различия характеристик у разных производителей, наиболее популярными остаются характеристики в форме окружности, четырехугольника и треугольника.
Рассмотрим характеристику “окружность”. Чтобы задать окружность на плоскости достаточно задать три точки, не лежащие на одной прямой. Точек может быть меньше, но тогда обязательным должно быть дополнительное условие, которое определит однозначность построения.
Например, для задания характеристики может быть заданы две уставки: полное сопротивление Z и угол линии φ (рис. 1).

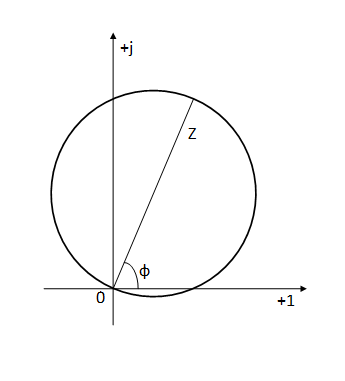
Этих данных недостаточно для построения характеристики. Из рисунка видно, что дополнительными условиями являются: окружность проходит через точку (0, 0), точки (0, 0), (Zcos(ф), Zsin(ф)) лежат на диаметре окружности.
Теперь данных достаточно, чтобы определить координаты центра (x0, y0) и радиус R. Ими соответственно являются (Zcos(ф)/2, Zsin(ф)/2) и Z/2.
Как определить, лежит точка с координатами (x,y) внутри или вне окружности? Ответ хорошо виден из следующего рисунка (рисунок 2).

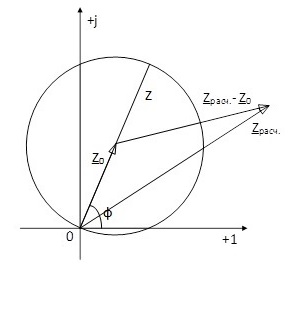
Необходимо, чтобы:

Или в ортогональных составляющих

Квадратный корень является ресурсоемкой операцией, и необходимости его извлечения для полного соответствия формул нет. Достаточно из уставок высчитать не радиус, а квадрат радиуса.
Рассмотри характеристику “четырехугольник” (рис. 3):

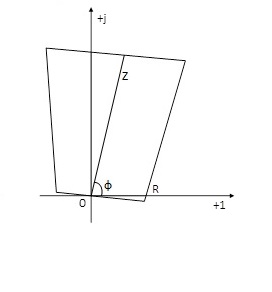
Характеристика ограничена четырьмя линиями, а уставок для настройки характеристики только три. Естественно, что должно быть достаточно дополнительных условий по наклону и положению сторон характеристики, на положение которых никак не влияют уставки доступные для изменения.
Для того, чтобы разобраться с четырехугольником, нужно понять, как определять положение точки относительно прямой.
Неравенство  ax + by ≥ c  определяет верхнюю полуплоскость, т.е. все точки верхней полуплоскости являются решением неравенства, а нижние нет. Граничная линия определяется превращением неравенства в равенство (рис. 4).

Таким образом, для определения положения точки относительно характеристики реле сопротивления надо определить положение точки относительно четырех прямых. Объединение условий по логическому «И» будет определять срабатывание реле сопротивления (рис. 5).

Найдем для примера уравнение стороны «1» – kx+b.
Коэффициент k равен тангенсу угла наклона прямой. Получаем k=tg(-5°)=-tg(5°). Из рисунка также видно, что эта прямая проходит через точку (Zcos(ф), Zsin(ф)). Тогда

Получаем уравнение первой стороны:

Из рисунка видно, что условием нахождения точки ниже первой стороны будет выполнение неравенства  f1(x) ≤ 0  при подстановке туда вместо x, y рассчитанных на данных момент активного и реактивного сопротивления (координаты точки в обозначениях сопротивлений будут записаны в виде (R, jX)). Важно не путать обозначение оси абсцисс x и обозначение реактивного сопротивления jX.

Используя такие же элементарные вычисления, можно получить уравнения оставшиеся уравнения сторон – f2(x), f3(x), f4(x). Тогда условием срабатывания реле сопротивления будет истинность логического выражения

В каждое из уравнений сторон необходимо подставить значения активного и реактивного сопротивлений в текущий момент времени.

Используя данные идеи, можно реализовать довольно тщательную проверку реле сопротивления с помощью устройства РЕТОМ. При автоматической проверке реле сопротивления выходными данными РЕТОМа являются два массива – массив углов (от 0° до 360°) с заранее заданным шагом и массив значений сопротивлений, при которых произошло срабатывание пускового органа. Экспортировав данные, например, в Excel, можно получить погрешности срабатывания в каждой точке, если в Excel корректно прописаны все формулы и углы перехода с одной стороны характеристики на другую.

Углы перехода рассчитываются также из уравнений. Формулы получаются громоздкими, но принципиально не сложнее, чем приведенные выше.

Результаты таких испытаний приведены на рисунках ниже. На рисунках синим показана теоретическая характеристика, а цветными маркерами – точки РЕТОМа (рис. 6, 7).

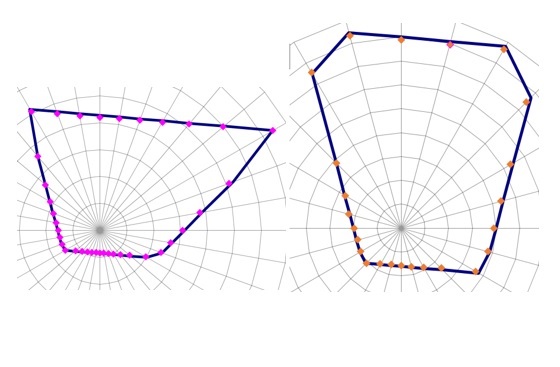
Пояснения к рисункам:

– При равномерном шаге по углу попасть в угол перехода с одной стороны на другую практически невозможно, поэтому может наблюдаться «срезание углов». В программе РЕТОМ есть очень полезная для этих целей функция «уточнение при переломе». При ее введении характеристика между изломами будет обработана с уменьшенным в 10 раз шагом.

– Даже без аналитического расчета погрешности видно, что экспериментальные точки ложатся очень близко к теоретическим прямым.

– Если Excel файл подготовлен заранее, то такие испытания не требуют практически ничего, кроме копирования данных из программы РЕТОМ в Excel.